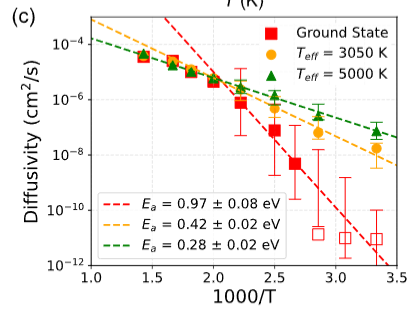
思考阿伦尼乌斯公式的起源,来源于对于固体电解质中随着温度改变,两种材料的离子电导率顺序会发生改变,也就是室温下那些相对有利的描述符在高温下变得相对有害;问题的根源来自离子电导率是温度的响应,或者说描述符是对温度的响应。响应的函数是活化能。活化能是本征不变的。
1. 绘制一个非log的阿伦尼乌斯公式
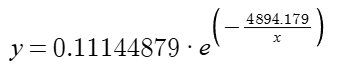
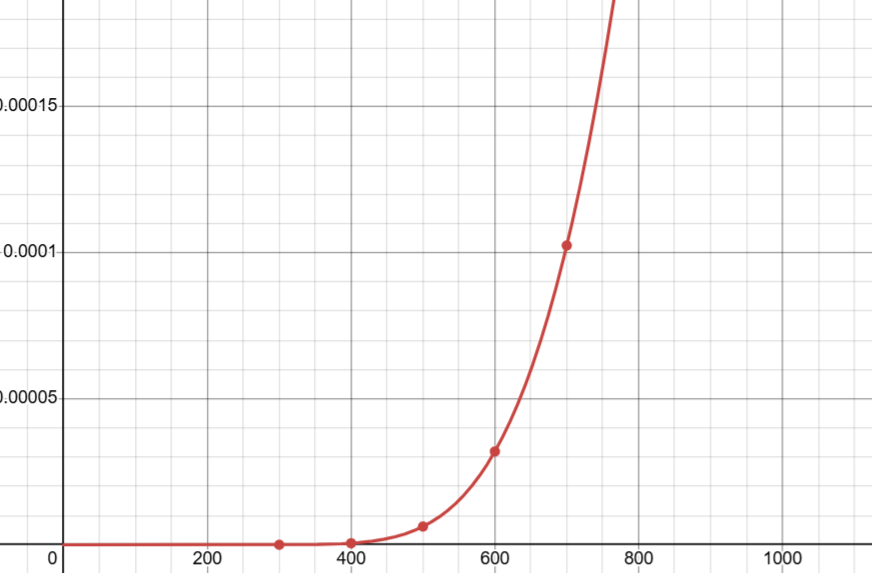
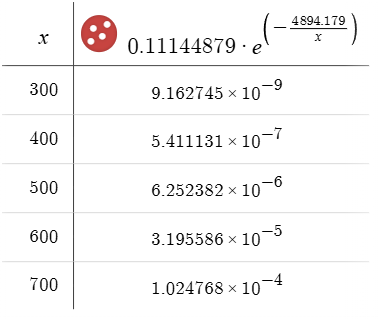
y=ae^(-b/x)的导数 $\frac{\partial f}{\partial x} = \frac{a,b,e^ {- \frac{b}{x} }}{x^2}$
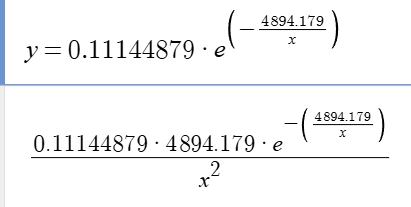
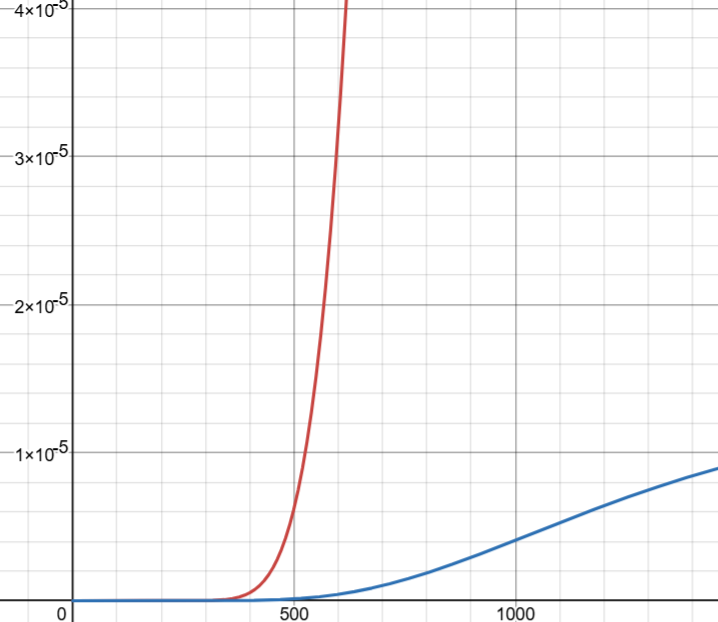
2. 麦克斯韦-玻尔兹曼分布
物理化学讲义 彭笑刚
1. 玻尔兹曼分布的含义
平衡态的概念:对于一个系统,在确定的外界条件下,应该有且只有一个平衡态,平衡态的表现是在系统的各个地方(当不考虑表界面时),其物理量不随时间有巨大的改变,但应该允许有涨落的存在。
平衡态只要求在系统的区域内其物理量不随时间有巨大改变,但并没有要求在不同的区域内物理量也相同,在表界面应该有梯度的存在,但是不同离子的化学势应该是平衡的。
在离子导体中的模拟中,或者在分子动力学的过程中,我们需要模拟的是平衡态的物理量,分子动力学中的收敛也是平衡态的含义。
对于一个宏观的孤立的离子导体,其内部的离子与表面处的离子应该是动态的平衡过程,或者表面到界面应该存在一个迁移的梯度,这种梯度的存在只是离子流的存在,但要求离子的化学势应该是平衡的。
对于每一个宏观状态,都对应着大量的微观状态。一个基本假设是所有的整体的微观状态都是等价的,具有相同的出现概率。宏观下的可观测的物理量,可以理解为微观状态的某个物理量的平均值
扩散系数应该就是这样一个物理量,应该是微观离子运动的距离和时间的平均值
时间平均值等价于系综平均值
计算msd时,理论上时间足够长,晶胞尺寸很小时也应该计算足够准确
扩散系数是一个在运动中才能观察到的物理量,但并不是一个运动中才能确定的物理量,其数值的静态统计部分在结构确定时,就应当由离子的振动频率和扩散距离决定,但是运动的离子的关联部分,需要在运动中得到统计平均
一个硬币抛1000次等于1000个硬币抛一次
1000个离子运动一次等于1个离子运动1000次
将N个粒子分配到n个能级上,第$i$个能级上的粒子数为$N_i$,可能的划分方式数量为
$$
w=\frac{N!}{\prod \limits_{i=0}^n N_i}
$$
晶格中离子的振动与输运是否也有不同的能级。宏观上看,输运处于平衡态时,扩散系数稳定,意味着其微观的离子所处的不同的能级/振幅的分布随时间是不变的(如果有这样的能级的话),这一平衡态也应该对应着大量的微观状态,也就是具体到每个粒子上,其所处的状态是不确定的,有大量可能的分布状态。
或许可以考虑从晶格静态结构中直接计算其(振幅)分布及分布的最可几状态,也就是平衡态,也就能计算扩散系数。不管非谐还是简谐,振动总是真实存在的,振幅也是真实存在的,或许非谐决定了分布的形状。
或许扩散系数有一个分布,而非谐、简谐决定了分布的样子,最可几分布就是宏观的扩散系数。当然,应该暂时不考虑运动中关联的效应
最可几态指的是微观状态数占据最大权重的宏观状态。在给定的外界条件下,系统的平衡态是系统的最可几态。
系统的元素数量越多,最可几态占据的权重越大。对一个真正宏观系统,当偏离最可几状态时,其状态所包含的微观状态数迅速下降到可以忽略不计。因此最可几状态是宏观系统的大部分时间能够观测到的。其他的涨落小到几乎不可观察
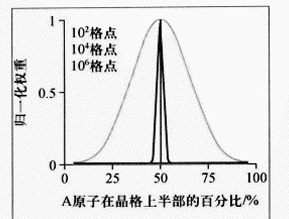
玻尔兹曼分布就是不同微观状态在外界环境下的分布状况
宏观状态之间有确定的稳定性差异,通过比较微观状态数的数量,可以判断两个宏观状态间的相对稳定性。以及判断一个化学/物理过程是否可以发生
离子从一个稳定态向另一个稳定态跳跃是一个过程,过程中需要跨越一个过渡态,能否到达过渡态是一次微观状态数的比较,从过渡态去哪里是另一次微观状态数的比较。说明过渡态的微观状态数是足够大的
记得有一篇文章提到过微观状态数和过渡态的关系
玻尔兹曼对熵的定义
$$
S=kln(W)
$$
$W$是微观状态数,微观状态数越多,权重越大,熵越大。熵是微观状态数的另一种描述
平衡态是微观状态数权重最大的状态,对应着也是熵最大的状态。系统向着平衡态演化
熵和微观状态数有相同的含义,在离子扩散过程中,是否可定义离子跳跃相关的熵。(振幅熵?)
统计物理中的熵增原理是一个自然而然的推论
在两个系统之间发生了能量的转移后,熵改变的难易程度,是由具体改变的能量与熵变来决定的。
温度是能量对熵的偏导数,描述了单位熵的改变需要的能量。
$$
T=(\frac{dU}{dS})_v,_n
$$
在离子输运中,也应该存在这样的定义,定义温度增加,可以允许的熵、即微观状态数的改变,这可能与温度升高,振动改变相关
3. 化学家眼中的阿伦尼乌斯公式
3. 阿伦尼乌斯公式的含义是什么
阿伦尼乌斯公式是经验公式,与之相似的是Eyring在1935年提出的Eyring equation,是建立在统计物理上的
一些参考资料
阿伦尼乌斯公式是如何推导出来的? - 查无此名12138的回答 - 知乎
https://www.zhihu.com/question/568999539/answer/2778592065
[非平衡态统计物理] 3 连续时间随机过程(四) - 笠道梓的文章 - 知乎
https://zhuanlan.zhihu.com/p/409136603
关于如图的Arrhenius方程,老师一定就让你们记住就行,但是我想知道这个方程当初是怎么得出来的? - 萌铁蛋 MnFeN的回答 - 知乎
https://www.zhihu.com/question/431586967/answer/1591685455
关于如图的Arrhenius方程,老师一定就让你们记住就行,但是我想知道这个方程当初是怎么得出来的? - 磷酸君Phosphates的回答 - 知乎
https://www.zhihu.com/question/431586967/answer/1591829506
关于如图的Arrhenius方程,老师一定就让你们记住就行,但是我想知道这个方程当初是怎么得出来的? - 太一的回答 - 知乎
https://www.zhihu.com/question/431586967/answer/1841701550
关于如图的Arrhenius方程,老师一定就让你们记住就行,但是我想知道这个方程当初是怎么得出来的? - BenderRodriguez的回答 - 知乎
https://www.zhihu.com/question/431586967/answer/1621985520
6.4.1: Eyring equation - Chemistry LibreTexts
https://public.websites.umich.edu/~elements/03chap/html/transition/index.htm#IV
转载请注明来源 有问题可通过github提交issue