晶格振动与声子

学习笔记

发布时间 : 2024-05-25 22:01

字数:2.4k

1.晶格振动和晶体热学性质
2.简正坐标声子
3. 态密度
4. 晶格热容
5. 固体物理 from simon
6.色散关系
7. 为什么声子态密度可以分元素画出来

1.晶格振动和晶体热学性质
2.简正坐标声子
3. 态密度
4. 晶格热容
5. 固体物理 from simon
6.色散关系
7. 为什么声子态密度可以分元素画出来

1.晶格振动和晶体热学性质

黄昆的《固体物理学》的第五章：晶格振动和晶体热学性质 - 知乎 (zhihu.com)

这里的简正坐标也可以看作简正原子的振动

简正坐标和坐标之间有变换关系

声子

2.简正坐标声子

固体物理：2.3 谐振子能量声子 - 知乎 (zhihu.com)

1. 广义坐标

1. 广义坐标就是在处理多物体的体系时，把整个体系看成一个物体，把多个物体（包括N自由度）的运动看成一个物体的不同部分在N维空间内的运动。但是区别于单个物体，一个体系物体内部的各部分的质量是不同的

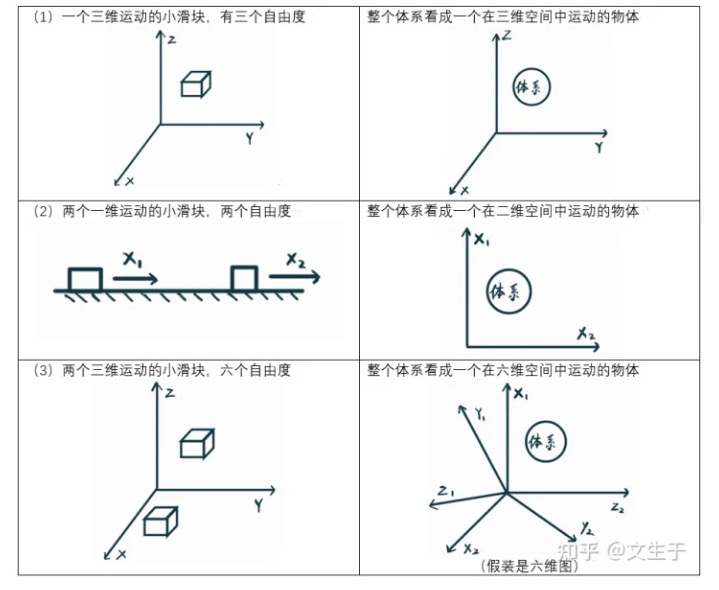
对于一个物体的能量，也可以按照自由度拆分为各个分能量

原子链中格波的表达式

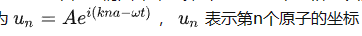
每个独立格波，都是一维单原子链的运动。体系的运动，就是多个格波的叠加

分运动的叠加是矢量叠加，需要给各个运动乘上对应方向的单位矢量

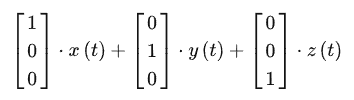
什么是坐标系：坐标系只不过是一种描述方式，只要找到两两不平行的一组向量，就能作为坐标系

其中，$k=m\frac{2\pi}{Na}, m=1-N$ 对应N个独立格波

这样，可以把一个格波中所有原子的坐标改写为（把振动作为基本坐标）

也就是只沿着第一个方向有分量。看成是整个个体的振动

2. 声子

==引入简正坐标就是为了引入不同简正模式的叠加==

经典理论中，谐振子的能量包括动能和势能

量子力学中，谐振子的能量为

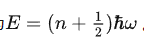
声子就是一个个的能量单元

3. 玻色爱因斯坦分布

晶体中的振动总能就是所有独立格波能量的累加，原子坐标就看成n个简正坐标的叠加

每个格波都对应着一定数量的声子

温度升高，所有格波的声子数都增加，温度下降，声子数减小，这也符合温度越大能量越高的判断

一个独立格波的平均能量就变成

T=0 K时，声子数趋近于零，但是格波的能量不为零，存在零点能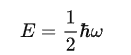

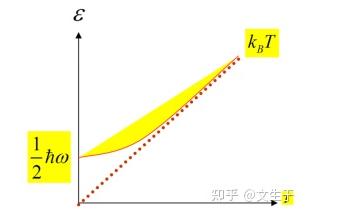
当温度很高时

这个时候一个格波的能量和温度T成正比

可以用来解决热容得问题，三维单原子链中有3N个独立格波

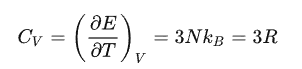
3. 态密度

独立格波的总数=总的自由度数=维数*原子数=原胞数*维数*单个原胞内的原子个数

绘制一张图，横坐标是频率，纵坐标是对应的能量

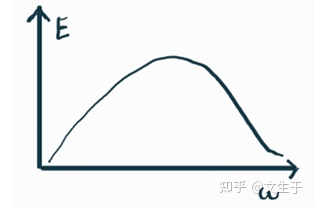
要计算总能，只需要对w积分，但是这里把无穷变为积分还需要打个补丁，考虑落在w-dw范围内的模式数是多少，也就是模式密度

给模式密度积分，就能得到独立格波总数

g(w)横坐标是w，纵坐标是不同的模式数

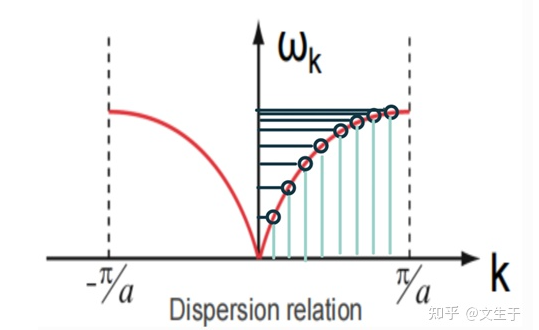
g(w)的值有些地方密集，有些地方分散每一处的模式密度都不同。模式密度处处不同，但是模式对应的波矢是均匀分布的。

==波矢空间的密度分布==

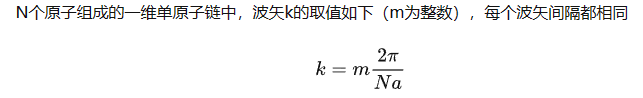
仿照g(w),可以定义一个单位波矢空间间隔内的振动模式数量，称为波矢密度

可以得到p(k)是一个常数

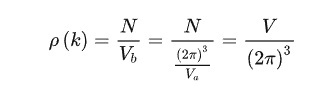
联系两个式子

例如

下面可以计算格波的总能量

色散关系很重要

4. 晶格热容

计算固体的热容，主要需要求声子的总能量。总能量等于各格波的能量叠加

确定态密度最关键的是知道色散关系

杜隆-波提

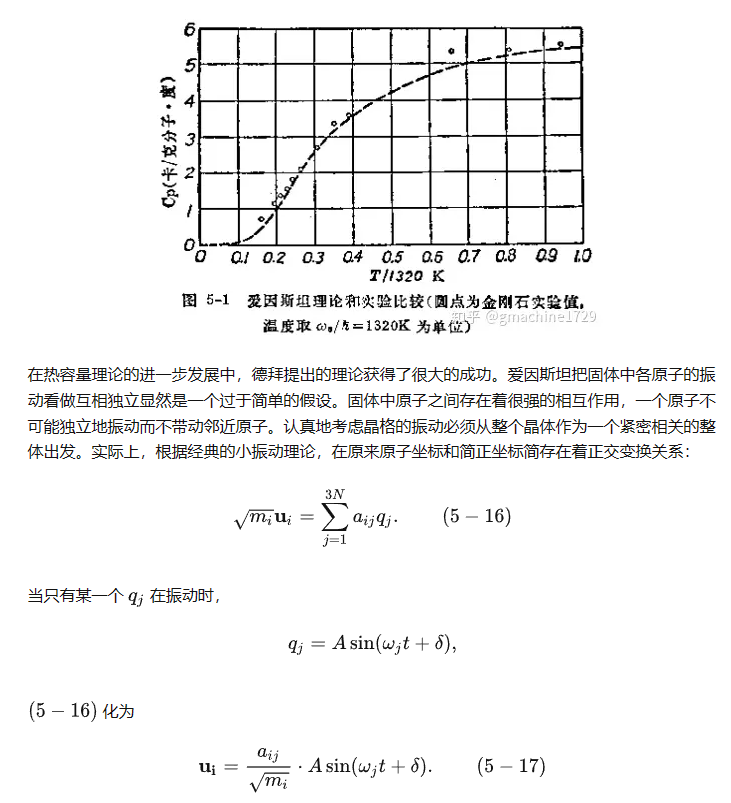
爱因斯坦模型直接定义有3N个谐振子（考虑了分布，有温度的效应）

德拜模型，考虑了线性的色散关系 w=cK （连续介质弹性波）

5. 固体物理 from simon

非简谐性质：非抛物线形状的势能曲线

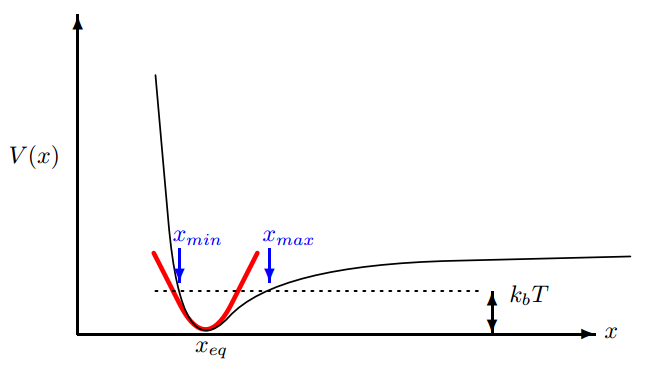
热膨胀：在温度升高时，x${max}$ 要大于x${min}$ ，导致原子间距离的平均值向右侧移动，晶格体积膨胀。平衡位置是能量最小值，但是不是原子振动的平均值（在小振动时由于是抛物线，所以相等，但是在高温下，不再是抛物线形状

==热膨胀本身对应着非简谐性==

6.色散关系

低频区对应着声学支，高频区对应着光学支(光学声子容易被光激发）。当波矢很小（即长波长）时，声子的频率通常与波矢成线性关系（通常叫做声波的“线性区域”），这是由于声子振动类似于经典的弹性波。

当波矢增大（即短波长）时，声子的频率趋于饱和，达到一个上限值，这通常与原子间的力常数以及晶体的弹性性质有关。

共有3N条色散关系，意味着每个k对应n个频率

声子态密度就是 g(w) ，如果一条w(k)是平的，就对应着这个能量区间有很多模式，那声子态密度就是一个大突出。

色散关系是本征的，可以根据色散关系对温度进行响应

能带也是本征的，根据相应电子色散进行响应

7. 为什么声子态密度可以分元素画出来

from matchat ai

[1] Chen J, et al. Real-Space Visualization of Frequency-Dependent Anisotropy of Atomic Vibrations. https://arxiv.org/abs/2312.01694

[2] Zhang L, et al. Multifield phonon spectrometrics of structured crystals and liquids. https://arxiv.org/abs/2001.02052

[3] Liu Y, et al. Normal modes in liquids and gases. https://arxiv.org/abs/2304.09778

[4] Wang H, et al. Algebraic theory of crystal vibrations: Singularities and zeros in vibrations of 1D and 2D lattices. https://arxiv.org/abs/1506.01707

[5] Smith R, et al. Density oscillations in multi-component molecular mixtures. https://arxiv.org/abs/0803.2950

[6] Li M, et al. Vibrational modes from MD simulation. https://arxiv.org/abs/2102.07957

[7] Zhao X, et al. Chapter 2: Normal mode decomposition of atomic motion in solids. https://arxiv.org/abs/2309.03140

8. 计算声子谱

来源

固体中简正模式的解释

力常数矩阵

每个原子的位移可以分为多个简谐振动的和 从这里可以计算力常数矩阵进而求出每个q的动力学矩阵，进而求出每个q的频率w，维度为3n

动力学矩阵

有限位移法（Finite Displacement Method）是一种用于计算晶体声子谱的数值方法，其基本原理是通过对晶体结构中的原子进行微小的位移，计算相应的力，从而构建力常数矩阵，进而求解声子频率和振动模式。

具体步骤如下：

结构优化：

首先，对晶体结构进行高精度的优化，以获得平衡的原子位置和晶格常数。
在优化过程中，需要设置适当的收敛标准，如能量收敛（EDIFF）和力收敛（EDIFFG）等，以确保结构的准确性。
构建超胞：

在优化后的结构基础上，使用Phonopy等工具构建超胞。
超胞的尺寸通常是原胞的整数倍，具体尺寸取决于所需的声子计算精度和计算资源。
原子位移：

对超胞中的每个原子进行微小的位移，通常在0.01到0.03埃之间。
这些位移可以是沿着晶体轴的正负方向，或者在不同方向上进行。
力计算：

在每个位移结构上，进行单点能量计算，获取每个原子所受的力。
这些力数据用于构建力常数矩阵。
构建力常数矩阵：

利用获得的力数据，构建力常数矩阵。
该矩阵描述了原子间的相互作用，是计算声子谱的基础。
声子谱计算：

通过对力常数矩阵进行对角化，得到声子的频率和振动模式。
进一步，可以绘制声子色散曲线，分析声子的行为。
注意事项：

有限位移法的计算精度高度依赖于力的计算精度，因此在结构优化和单点计算中需要设置严格的收敛标准。
位移幅度的选择需要平衡计算精度和计算量，过大的位移可能导致力常数矩阵的非线性，过小的位移可能导致数值误差。
计算过程中，可能需要考虑晶体的对称性，以减少计算量。
通过上述步骤，有限位移法能够有效地计算晶体的声子谱，为研究材料的热力学性质、动力学稳定性等提供重要信息。