1.电池负极比容量计算

法拉第常数:96485 C/mol
含义:1mol电子的带电量
*6.0210^23 * 1.6 10^-19*
2. 阿伦尼乌斯关系式辨析
关于电导率和温度倒数的图像,目前有两种画法,分别是
$log(\sigma T)与\frac{1}{T}$和$log(\sigma)与1/T$
根据公式
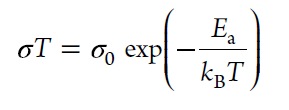
绘制$log(\sigma T)与$$\frac{1}{T}$的关系是正确的
为什么一些计算用$log(\sigma)$与温度倒数仍能得到不错的结论呢
$log(\sigma T)=log(\sigma )+log(T)$,相当于在log(σ)的基础上每个点加上log(T)项,而log(T)项,在几百k的温度下,变化幅度并不大,所以能够得到相近的活化能。

由于更高温度log(T)带来的增幅更大, 所以log(σT)得到的活化能要比log(σ)更大
σ的值通常在1附近。
尤其对于实验,很难做特别大温度范围内的测量,通常温度幅度只有几十K,这样,使用log(σT)和log(σ)能够得到完全一致的活化能。
==对于计算,由于温度变化幅度很大,因此必须要用log(σT),对于实验,温度范围不大的话,而且与要探测的温度差距不大的话,无所谓了,当然,用log(σT)肯定是对的。==
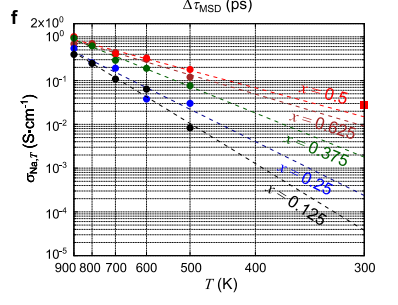
以这篇文章(Adv. Funct. Mater. 2022, 32, 2206036)的黑色点为例,文中给的是log(σ),得到的值为
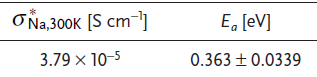
使用数据重新作图后得到
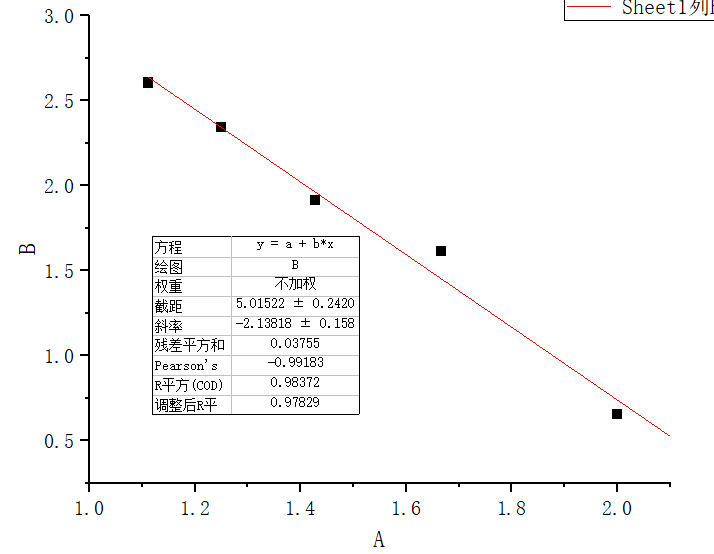
Ea = 0.4248 eV σ300=2.58*10^-5 S/cm
- 首次充放电、高倍率下的低容量、充放电曲线
3. 关于扩散系数的尺寸效应
转载请注明来源 有问题可通过github提交issue