1.分子动力学本身的理论
1. 关于温度波动与smass值


ceder的关于smass为0的文章 :



2. 理论理解
参考文献:
声子零点振动能(ZPE)和吉布斯自由能的理论推导及VASP计算实操(一) (qq.com)
1.能量的区分
- 能量分为体系的内能U、焓H、吉布斯自由能G
其中
$G=U+PV-TS$
$H=U+PV$
内能等于
$U=E_{electron}+ZPE$
其中,E_electron是电子总能,ZPE是声子的零点振动能
==vasp中,使用grep withoutentropy OUTCAR得到的能量就只是电子总能==
因为第一性原理计算没有温度,所以不包括体系的动能项
零点振动能对于较轻元素的体系(H He Li)的体系需要考虑,对于较重的元素,ZPE远远小于E_electron,通常不考虑
讨论吉布斯自由能
吉布斯自由能中有熵
$S=S_k+S_{vib}+S_{elec}$
其中S_k是构型熵,S_vib是振动熵(一般温度下贡献较小,第一性原理计算中未考虑),S_elec是电子熵
2. 声子振动能和振动熵、零点振动能
声子作为准粒子来看,借助玻尔兹曼分布和准粒子的概念
一个材料体系,可以看作是由声子和电子组成,材料体系的总能是电子总能与声子总能之和
电子总能包括电子间相互作用能,原子核对电子的作用,范德华相互作用(均包括在grep without OUTCAR)中,和电子熵对总能的贡献(未包括)
第一性原理计算不能包括振动的能量
声子总能包括声子内能(振动能)和振动熵的贡献,零点振动能是声子总能的一部分(从下面的推导中可见)。第一性原理计算通常只能计算出声子的本征振动模(振动频率),而声子的ZPE和吉布斯自由能需要结合统计力学处理得到。

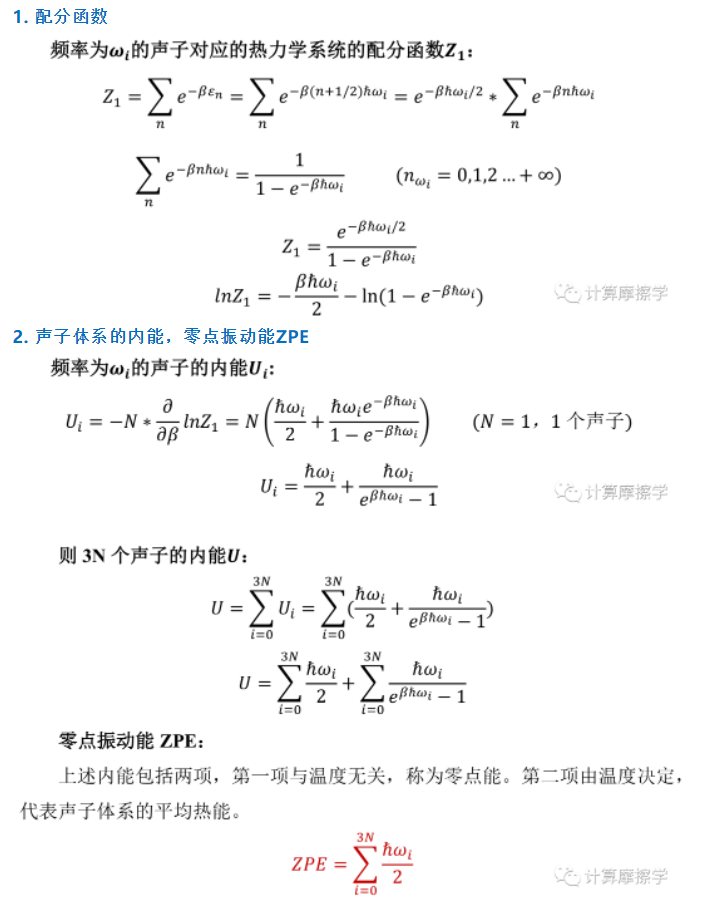

3.vasp计算声子振动能和振动熵
vasp可以直接计算出材料的振动熵



4. 构型熵的计算



3.可以利用的计算
1. 振动熵
Influence of Lattice Dynamics on Na+ Transport in the Solid Electrolyte Na3PS4−xSex
How Chemical Composition Alone Can Predict Vibrational Free Energies and Entropies of Solids
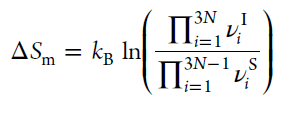
2.声子带心(phonon band center) (标识平均振动频率)
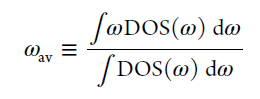
3. 配分声子DOS和总声子DOS -速度自关联函数的的傅里叶变换
Extreme phonon anharmonicity underpins superionic diffusion and ultralow thermal conductivity in argyrodite Ag8SnSe6
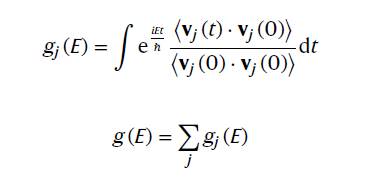
转载请注明来源 有问题可通过github提交issue