1.学习统计力学
学习统计力学
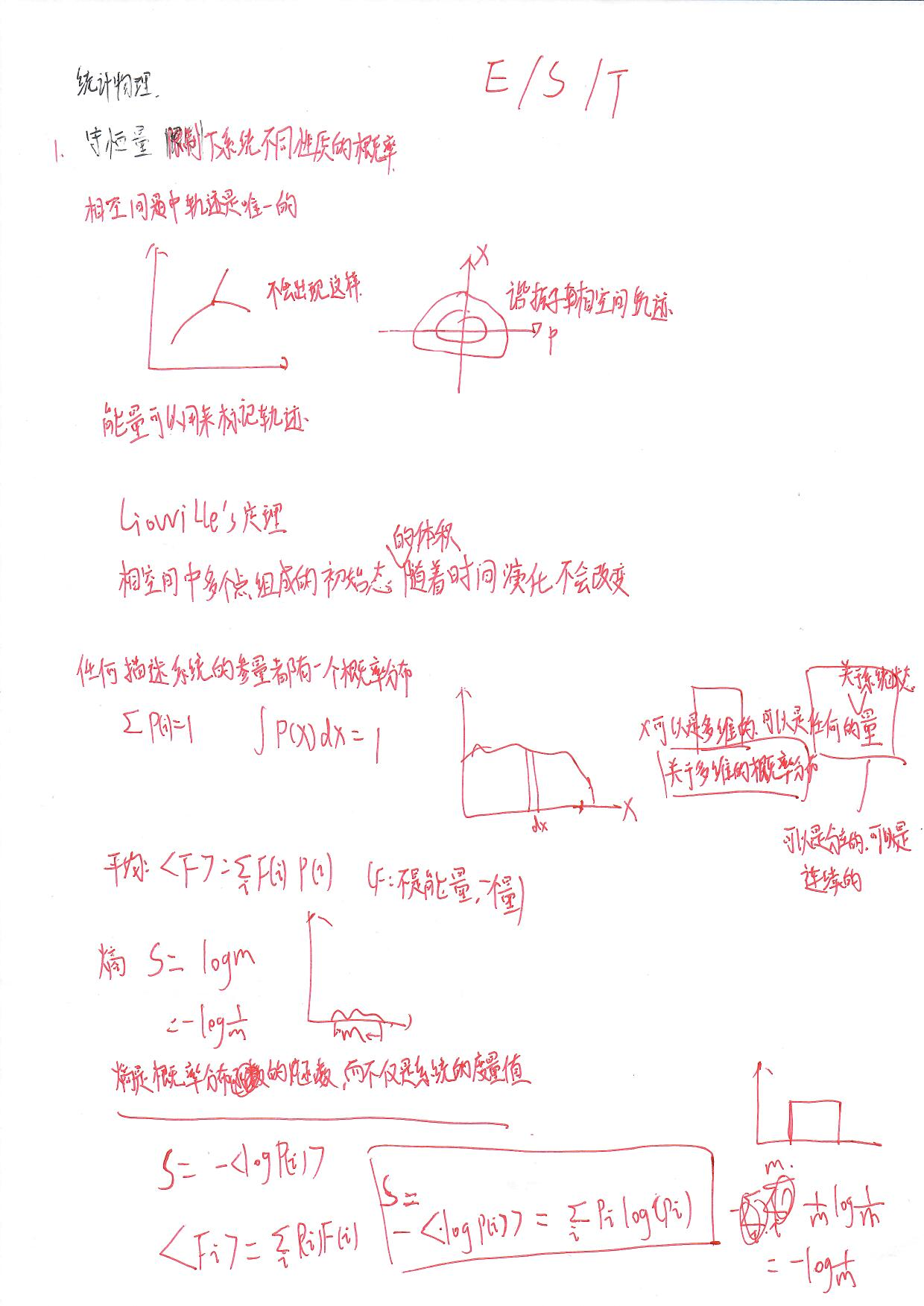

势能面本质上是多维的能量概率分布

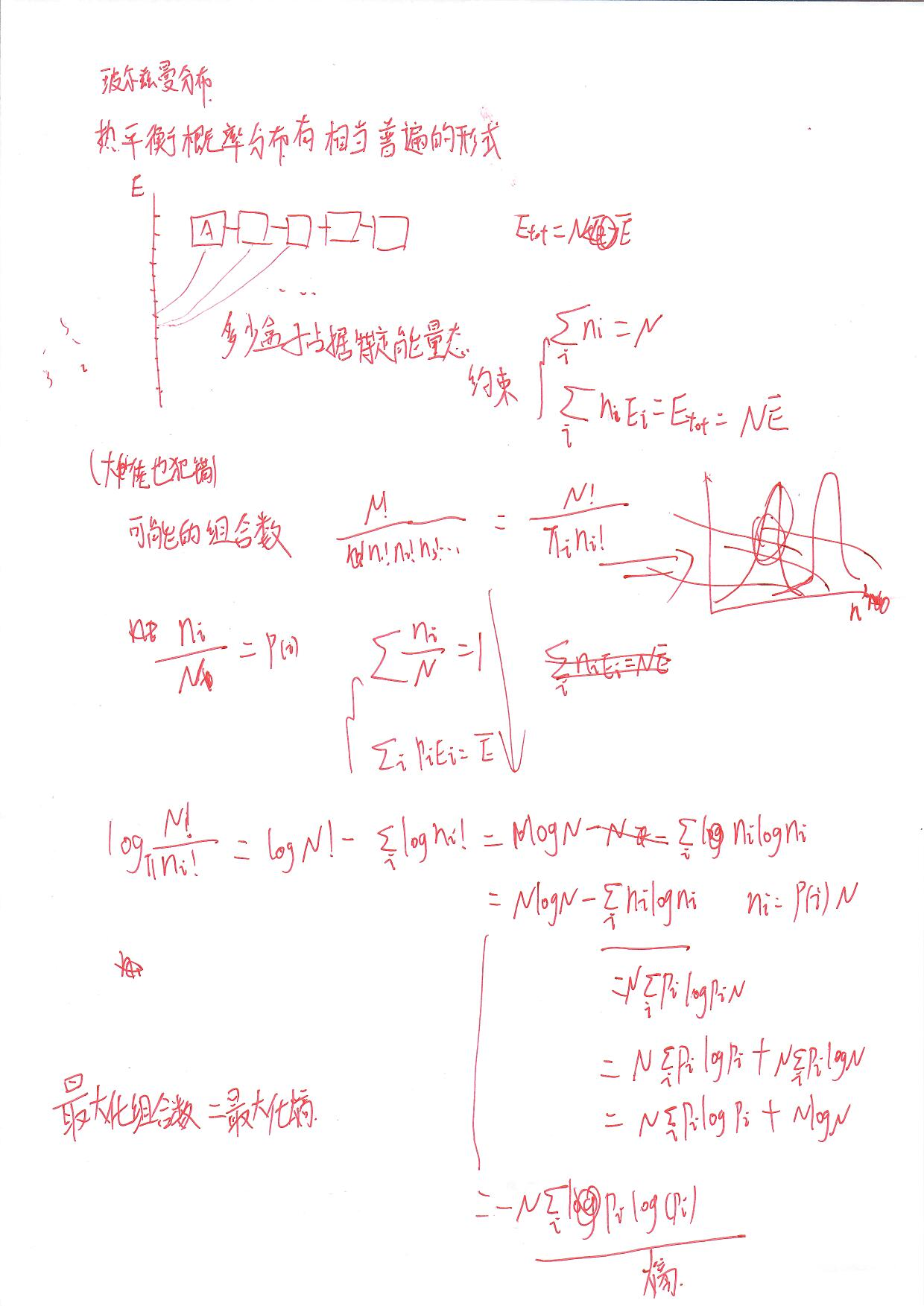
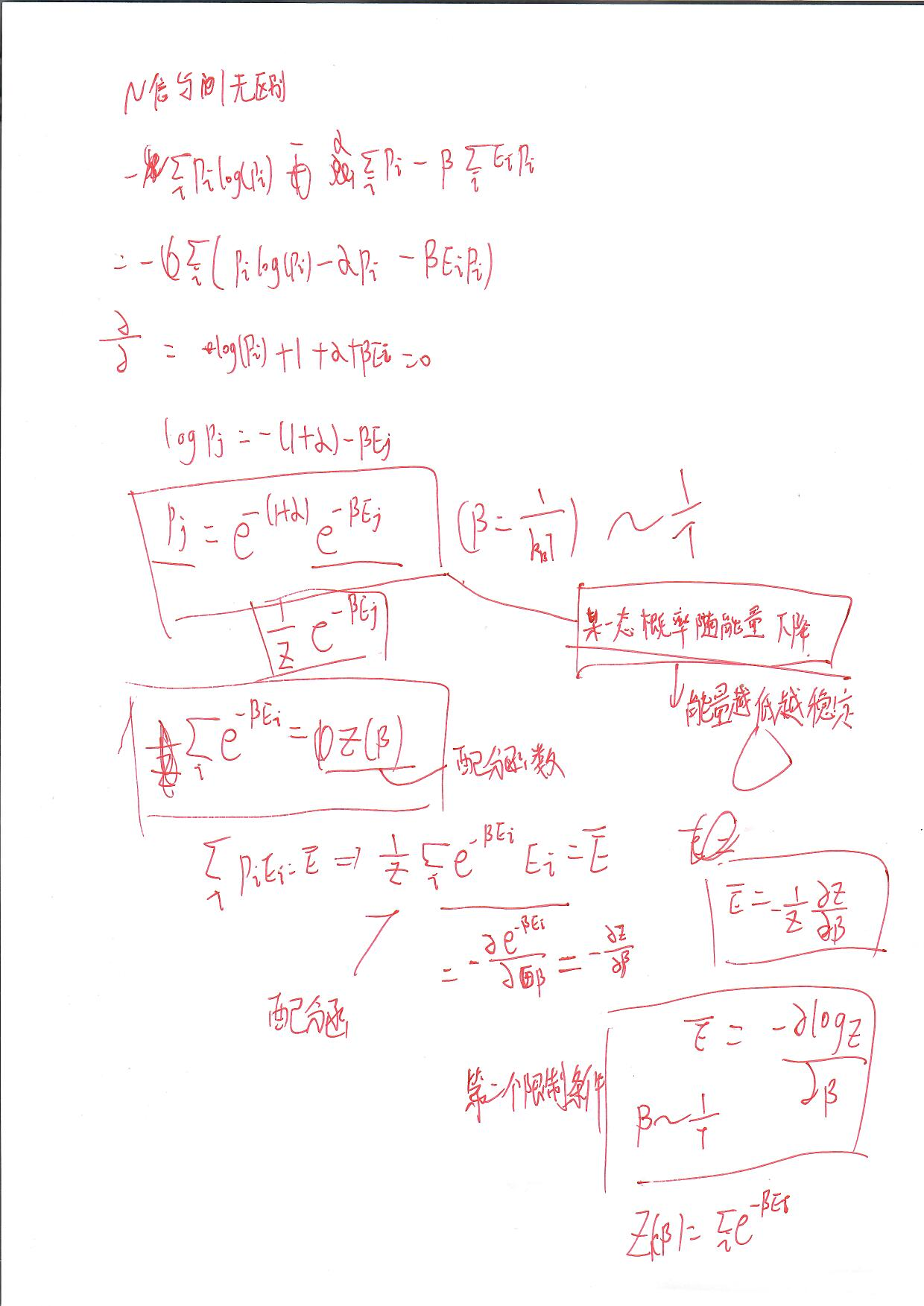

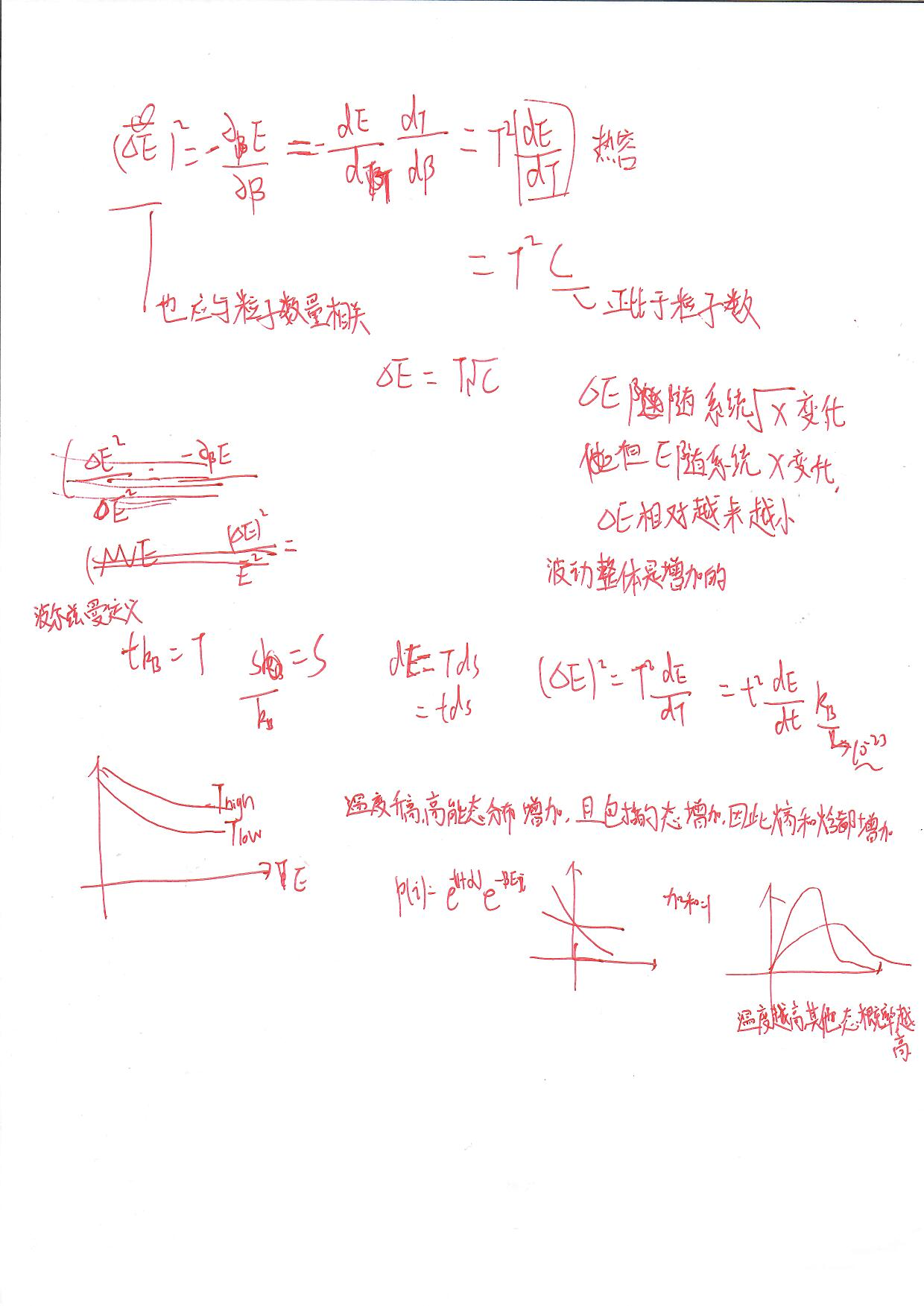
2. 如何用统计物理理解晶体
2.1 晶体与统计物理中微观态的关系
对于一个有大量原子的集合,可以有多种微观状态,晶体也是其中一种微观状态,且能量比普通随机的微观状态低得多,因此是概率最大的微观状态。温度升高时,系统的状态由能量和熵共同决定,高温下无序状态的熵贡献可能使系统偏离晶体结构。结构熔化就是一种温度升高导致的能量最小值改变的现象。
宏观态指的是宏观的外界条件,微观态指的是宏观条件约束下原子的速度、坐标等信息
2.2 两者的不同
统计物理描述的是大量微观状态/粒子在不同能级上的分布,晶体中的声子、电子能级、空位浓度这些描述在不同能级上的分布可以用统计物理来理解。
但是晶体在基态时是能量最低的状态,这与统计力学不同,统计物理中,平衡态并不是能量最低的状态,而是微观状态数最多的状态。可以理解为平衡态下,晶体中的声子的分布并不是能量最低的状态,而是有最合适的分布。
空位浓度是统计物理的研究范围,离子的扩散也是空位的浓度的一种重分布啊(阿伦尼乌斯公式)
2.3 统计物理来理解晶格中的声子
在统计物理中,声子是描述晶体中原子集体振动的量子化准粒子。理解声子和它们在不同温度下的行为可以揭示晶体的热力学性质、比热容、热导率等。
声子的统计物理描述
1. 声子基本概念
- 声子: 声子是晶格振动的量子化模式。声子可以分为纵波和横波,且每种类型可以进一步分为声学声子和光学声子。
- 简谐振动: 在平衡位置附近,原子的振动可以近似为简谐振动。这个近似使得我们能够用二次项展开势能函数,并使用量子力学来处理振动能级。
2. 声子模型和配分函数
在统计物理中,声子的贡献通过声子配分函数来描述。对于一个具有频率 $( \omega_q)$ 的声子模式,其能量量子化为:
$$[ E_n = \left( n + \frac{1}{2} \right) \hbar \omega_q ]$$
其中 $$( n = 0, 1, 2, \ldots )$$。
对于一组声子模式,配分函数$$ ( Z_{\text{phonon}} )$$ 可以写成:
$$[ Z_{\text{phonon}} = \prod_{q} \left( \sum_{n_q=0}^{\infty} e^{-\beta \left( n_q + \frac{1}{2} \right) \hbar \omega_q} \right) ]$$
计算上述和,可以得到:
$$[ Z_{\text{phonon}} = \prod_{q} \left( \frac{e^{-\beta \hbar \omega_q / 2}}{1 - e^{-\beta \hbar \omega_q}} \right) ]$$
3. 声子的热力学性质
通过声子配分函数,可以计算出系统的热力学性质:
内能 ( U ):
$$[ U = \sum_q \left( \frac{\hbar \omega_q}{2} + \frac{\hbar \omega_q}{e^{\beta \hbar \omega_q} - 1} \right) ]$$其中,第一项是零点能,第二项是由热激发引起的能量。
比热容 ( C_V ):
$$[ C_V = \left( \frac{\partial U}{\partial T} \right)_V ]$$
对于高温(经典极限)和低温(量子极限),比热容表现出不同的行为。在低温下,比热容 ( C_V ) 随温度 ( T ) 的立方关系增长(德拜定律);在高温下,比热容趋于常数(德拜高温极限)。
温度升高时晶体的振动变化
1. 低温下的振动
在低温下,大多数声子模式处于其最低量子态,只有少量的声子被激发。这时,晶体的热容量主要由少数低频声子(长波长声子)贡献。热激发的能量较少,原子振动幅度较小。
2. 高温下的振动
随着温度升高,更多的声子模式被热激发,占据更高的量子态。这导致以下几方面的变化:
声子激发增加:
高温下,大量声子被激发,声子模式的占据数增加。这意味着晶体内的原子振动更加剧烈。平均振动能量增加:
根据玻尔兹曼分布,声子的平均能量随温度增加。高温下,每个声子模式的平均能量趋近于 ( k_B T )。比热容趋于常数:
在经典极限(高温下),根据德拜模型,晶体的比热容趋于 ( 3Nk_B ),其中 ( N ) 是原子的数目。这称为德拜高温极限。
德拜模型
德拜模型是描述声子热容的经典模型之一。德拜模型假设声子的频谱是连续的,并引入一个最高截止频率 (\omega_D),即德拜频率。
德拜频率:
$$[ \omega_D^3 = \frac{6\pi^2 N}{V} v_s^3 ]$$其中, ( v_s ) 是声速, ( N ) 是晶体中的原子数, ( V ) 是体积。
德拜积分:
德拜模型中,比热容 ( C_V ) 可以通过德拜积分计算:$$[ C_V = 9Nk_B \left( \frac{T}{\Theta_D} \right)^3 \int_0^{\Theta_D/T} \frac{x^4 e^x}{(e^x - 1)^2} dx ]$$
其中, $$(\Theta_D = \hbar \omega_D / k_B) $$是德拜温度。
结论
通过统计物理和声子模型,可以理解晶体的振动行为及其热力学性质。随着温度升高,晶体的原子振动加剧,声子激发增加,比热容从低温下的$$ ( T^3 )$$ 依赖逐渐趋于常数。这些行为在德拜模型和配分函数的框架下得到了很好的解释。
3. 玻尔兹曼分布与麦克斯韦-玻尔兹曼分布函数

玻尔兹曼分布既指某一个宏观状态的概率,也可指某个全同小部分的概率的分布
转载请注明来源 有问题可通过github提交issue